The Parallax Principle

First, how do we know that the nearest stars are so far away? For that matter, how do we know how far away any stars are? We’ve come a long way in this blog, and, on our journey, we have spoken a good deal about distances—by earthly standards, often extraordinary distances. Indeed, the distances astronomers measure are so vast that they use a set of units unique to astronomy. When measuring distances on the earth, meters and kilometers are convenient units. But in the vast spaces between stars and galaxies, such units are inadequate. As we’ll see in this chapter and those that follow, the way astronomers measure distances, and the units they use depend upon how far away the objects are. Distances between a given point on the earth and many objects in the solar system can be measured by radar ranging. Radar, a technology developed shortly before and during World War II, is now quite familiar. Radar can be used to detect and track distant objects by transmitting radio waves, then receiving the echo of the waves the object bounces back (sonar is a similar technique using sound waves). If we multiply the round-trip travel time of the outgoing signal and its incoming echo by the speed of light (which, you’ll recall, is the speed of all electromagnetic radiation, including radio waves), we obtain a figure that is twice the distance to the target object.
Radar ranging works well with objects that return (bounce back) radio signals. But stars, including our sun, tend to absorb rather than return electromagnetic radiation transmitted to them. Moreover, even if we could bounce a signal off a star, most are so distant that we would have to wait thousands of years for the signal to make its round trip—even at the speed of light! Even the nearby Alpha Centauri system would take about eight years to detect with radar ranging, were it even possible.
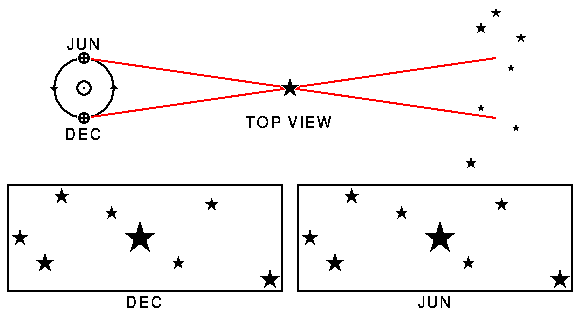
Another method is used to determine the distance of the stars, a method that was available long before World War II. In fact, it is at least as old as the Greek geometer Euclid, who lived in the third century B.C.E. The technique is called triangulation—an indirect method of measuring distance derived by geometry using a known baseline and two angles from the baseline to the object. Triangulation does not require a right triangle, but the establishment of one 90-degree angle does make the calculation of distance a bit easier. It works like this. Suppose you are on one rim of the Grand Canyon and want to measure the distance from where you are standing to a campsite located on the other rim. You can’t throw a tape measure across the yawning chasm, so you must measure the distance indirectly. You position yourself directly across from the campsite, mark your position, then turn 90 degrees from the canyon and carefully pace off another point a certain distance from your original position. This distance is called your baseline. From this second position, you sight on the campsite. Whereas the angle formed by the baseline and the line of sight at your original position is 90 degrees (you arranged it to be so), the angle formed by the baseline and the line of sight at the second position will be somewhat less than 90 degrees. If you connect the campsite with Point A (your original viewpoint) and the campsite with Point B (the second viewpoint), both of which are joined by the baseline, you will have a right triangle. Now, you can take this right triangle and, with a little work, calculate the distance across the canyon. If you simply make a drawing of your setup, making sure to draw the angles and lengths that you know to scale, you can measure the distance across the canyon from your drawing. Or if you are good at trigonometry, you can readily use the difference between the angles at Points A and B and the length of the baseline to arrive at the distance to the remote campsite.