How Far Away Are the Stars?

Like the campsite separated from you by the Grand Canyon, the stars are not directly accessible to measurement. However, if you can establish two view points along a baseline, you can use triangulation to measure the distance to a given star.
There is just one problem.
Take a piece of paper. Draw a line one inch long. This line is the baseline of your triangle. Measure up from that line, say, one inch, and make a point. Now connect the ends of your baseline to that point. You have a nice, normal looking triangle. But if you place your point several feet from the baseline, then connect the ends of the baseline to it, you will have an extremely long and skinny triangle, with angles that are very difficult to measure accurately, because they will both be close to 90 degrees. If you move your point several miles away, and keep a 1-inch baseline, the difference in the angles at Points A and B of your baseline will be just about impossible to measure. They will both seem like right angles. For practical purposes, a 1-inch baseline is just not long enough to measure distances of a few miles away. Now recall that if our Earth is a golf ball (about 1 inch in diameter), that the nearest star, to scale, would be 50,000 miles away. So the baseline created by, say, the rotation of the earth on its axis—which would give 2 points 1 inch away in our model—is not nearly large enough to use triangulation to measure the distance to the nearest stars. The diameter of the earth is only so wide. How can we extend the baseline to a useful distance?
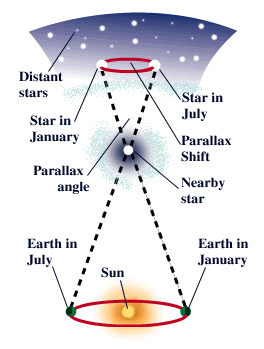
The solution is to use the fact that our planet not only rotates on its axis, but also orbits the sun. Observation of the target star is made, say, on February 1, then is made again on August 1, when the earth has orbited 180 degrees from its position six months earlier. In effect, this motion creates a baseline that is 2 A.U. long—that is, twice the distance from the earth to the sun. Observations made at these two times (and these two places) will show the target star apparently shifted relative to the even more distant stars in the background. This shift is called stellar parallax, and by measuring it, we can determine the angle relative to the baseline and thereby use triangulation to calculate the star’s distance.
To get a handle on parallax, hold your index finger in front of you, with your arm extended. Using one eye, line up your finger with some vertical feature, say the edge of the window. Now, keeping you finger where it is, look through the other eye. The change in viewpoint makes your finger appear to move with respect to a background object. In astronomy, your eyes are the position of the earth separated by 6 months, your finger is a nearby star, and the window edge is a distant background star. This method works as long as the star (your finger) is relatively close. If the star is too far away, parallax is no longer effective.