Creating a Star Scale of Magnitude

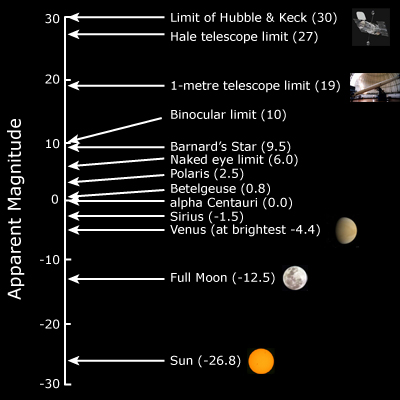
So astronomers have learned to be very careful when classifying stars according to apparent brightness. Classifying stars according to their magnitude seemed a good idea to Hipparchus (in the second century B.C.E.) when he came up with a 6-degree scale, ranging from 1, the brightest stars, to 6, those just barely visible. Unfortunately, this somewhat cumbersome and awkward system (higher magnitudes are fainter, and the brightest objects have negative magnitudes) has persisted to this day.
Hipparchus’ scale has been expanded and refined over the years. The intervals between magnitudes have been regularized, so that a difference of 1 in magnitude corresponds to a difference of about 2.5 in brightness. Thus, a magnitude 1 star is 2.5 ×2.5 ×2.5 ×2.5 ×2.5=100 times brighter than a magnitude 6 star. Because we are no longer limited to viewing the sky with our eyes, and larger apertures collect more light, magnitudes greater than (that is, fainter than) 6 appear on the scale. Objects brighter than the brightest stars may also be included, their magnitudes expressed as negative numbers. Thus the full moon has a magnitude of –12.5 and the sun, –26.8. In order to make more useful comparisons between stars at varying distances, astronomers differentiate between apparent magnitude and absolute magnitude, defining the latter, by convention, as an object’s apparent magnitude when it is at a distance of 10 parsecs from the observer. This convention cancels out distance as a factor in brightness and is therefore an intrinsic property of the star.